Memahami KPK dan FPB: Panduan Lengkap dengan Contoh Soal untuk Kelas 4 SD

Memasuki kelas 4 SD, matematika menjadi semakin menarik dan menantang. Salah satu materi penting yang akan dipelajari adalah tentang Kelipatan Persekutuan Terkecil (KPK) dan Faktor Persekutuan Terbesar (FPB). Konsep ini sangat penting untuk dipahami karena akan menjadi dasar untuk mempelajari materi matematika yang lebih kompleks di kelas-kelas selanjutnya, seperti pecahan, aljabar, dan lainnya.

Artikel ini akan membahas secara mendalam tentang KPK dan FPB, lengkap dengan contoh soal dan cara penyelesaiannya yang mudah dipahami. Dengan panduan ini, diharapkan siswa kelas 4 SD dapat menguasai materi ini dengan baik dan merasa lebih percaya diri dalam belajar matematika.

Apa itu Kelipatan Persekutuan Terkecil (KPK)?

KPK adalah bilangan terkecil yang merupakan kelipatan dari dua bilangan atau lebih. Secara sederhana, KPK adalah angka yang bisa dibagi habis oleh semua bilangan yang dicari KPK-nya.

Contoh:

• Kelipatan 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, …
• Kelipatan 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, …

Kelipatan persekutuan dari 2 dan 3 adalah: 6, 12, 18, …

Dari kelipatan persekutuan tersebut, yang terkecil adalah 6. Jadi, KPK dari 2 dan 3 adalah 6.

Cara Mencari KPK:

Ada beberapa cara untuk mencari KPK, antara lain:

1. Mencari Kelipatan: Seperti contoh di atas, kita mencari kelipatan dari setiap bilangan sampai menemukan kelipatan yang sama. Cara ini efektif untuk bilangan yang kecil.
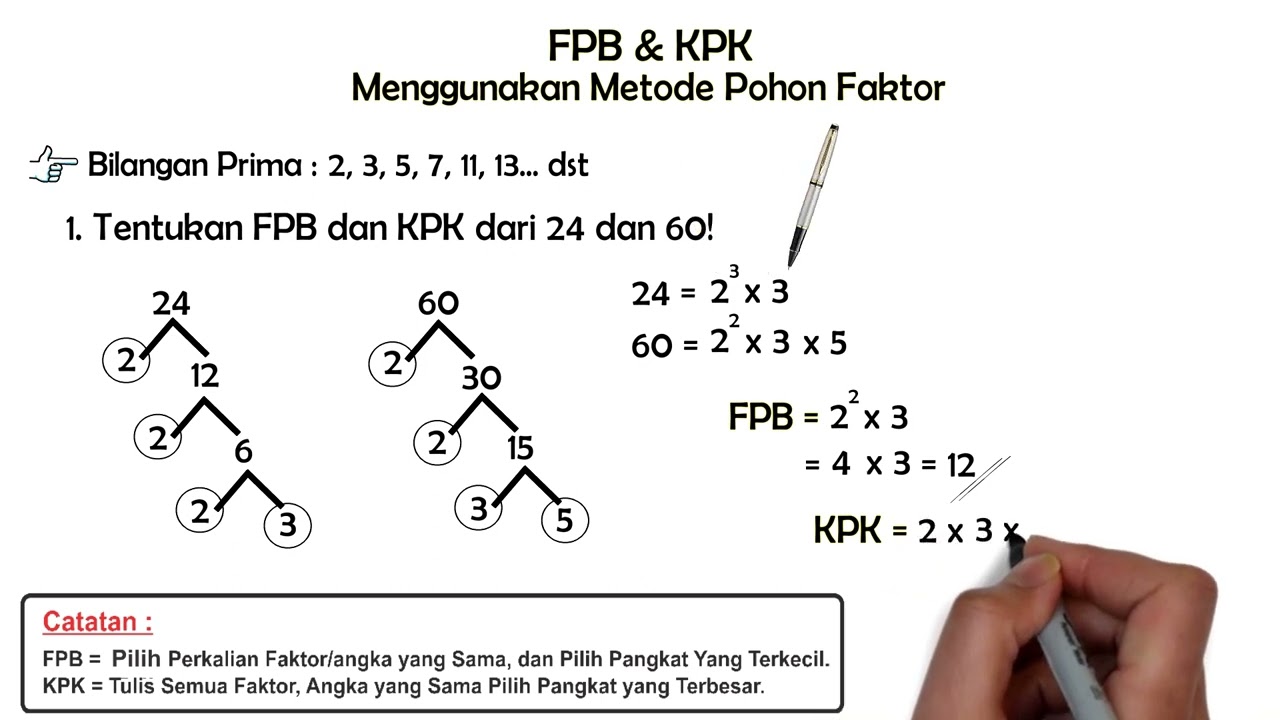
2. Menggunakan Pohon Faktor: Cara ini lebih efektif untuk bilangan yang lebih besar.
   • Buat pohon faktor untuk setiap bilangan.
   • Tuliskan faktorisasi prima dari setiap bilangan.
   • KPK didapatkan dengan mengalikan semua faktor prima yang ada, dengan mengambil pangkat tertinggi jika ada faktor prima yang sama.
3. Menggunakan Tabel: Buat tabel dengan bilangan-bilangan yang akan dicari KPK-nya sebagai kolom. Bagi semua bilangan dengan bilangan prima terkecil (biasanya dimulai dengan 2). Jika ada bilangan yang tidak bisa dibagi, tuliskan kembali bilangan tersebut. Lanjutkan pembagian dengan bilangan prima berikutnya sampai semua bilangan menjadi 1. KPK adalah hasil perkalian semua bilangan prima yang digunakan untuk membagi.

Contoh Soal KPK:

1. Soal: Tentukan KPK dari 4 dan 6!

   Penyelesaian (Menggunakan Pohon Faktor):

   • Pohon Faktor 4: 4 -> 2 x 2 = 2²
   • Pohon Faktor 6: 6 -> 2 x 3

   Faktorisasi Prima:

   • 4 = 2²
   • 6 = 2 x 3

   KPK = 2² x 3 = 4 x 3 = 12

   Jadi, KPK dari 4 dan 6 adalah 12.

2. Soal: Tentukan KPK dari 8 dan 12!

   Penyelesaian (Menggunakan Tabel):

   Bilangan Prima	8	12
   2	4	6
   2	2	3
   2	1	3
   3	1	1

   KPK = 2 x 2 x 2 x 3 = 24

   Jadi, KPK dari 8 dan 12 adalah 24.

Apa itu Faktor Persekutuan Terbesar (FPB)?

FPB adalah bilangan terbesar yang dapat membagi habis dua bilangan atau lebih. Secara sederhana, FPB adalah angka terbesar yang bisa digunakan untuk membagi semua bilangan yang dicari FPB-nya.

Contoh:

• Faktor 12: 1, 2, 3, 4, 6, 12
• Faktor 18: 1, 2, 3, 6, 9, 18

Faktor persekutuan dari 12 dan 18 adalah: 1, 2, 3, 6

Dari faktor persekutuan tersebut, yang terbesar adalah 6. Jadi, FPB dari 12 dan 18 adalah 6.

Cara Mencari FPB:

Ada beberapa cara untuk mencari FPB, antara lain:

1. Mencari Faktor: Seperti contoh di atas, kita mencari faktor dari setiap bilangan sampai menemukan faktor yang sama. Cara ini efektif untuk bilangan yang kecil.
2. Menggunakan Pohon Faktor: Cara ini lebih efektif untuk bilangan yang lebih besar.
   • Buat pohon faktor untuk setiap bilangan.
   • Tuliskan faktorisasi prima dari setiap bilangan.
   • FPB didapatkan dengan mengalikan faktor prima yang sama, dengan mengambil pangkat terendah jika ada faktor prima yang sama.
3. Menggunakan Algoritma Euclid: Cara ini lebih efisien untuk bilangan yang sangat besar. Algoritma Euclid dilakukan dengan membagi bilangan yang lebih besar dengan bilangan yang lebih kecil. Kemudian, bilangan yang lebih kecil dibagi dengan sisa hasil pembagian sebelumnya. Proses ini diulang sampai sisanya menjadi 0. FPB adalah pembagi terakhir sebelum sisanya menjadi 0.

Contoh Soal FPB:

1. Soal: Tentukan FPB dari 16 dan 24!

   Penyelesaian (Menggunakan Pohon Faktor):

   • Pohon Faktor 16: 16 -> 2 x 2 x 2 x 2 = 2⁴
   • Pohon Faktor 24: 24 -> 2 x 2 x 2 x 3 = 2³ x 3

   Faktorisasi Prima:

   • 16 = 2⁴
   • 24 = 2³ x 3

   FPB = 2³ = 8

   Jadi, FPB dari 16 dan 24 adalah 8.

2. Soal: Tentukan FPB dari 36 dan 48!

   Penyelesaian (Mencari Faktor):

   • Faktor 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
   • Faktor 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48

   Faktor persekutuan: 1, 2, 3, 4, 6, 12

   FPB = 12

   Jadi, FPB dari 36 dan 48 adalah 12.

Kapan Menggunakan KPK dan FPB?

KPK dan FPB sering digunakan dalam kehidupan sehari-hari untuk menyelesaikan masalah yang berkaitan dengan pengulangan, pembagian, atau pengelompokan.

Contoh Penggunaan KPK:

• Menentukan waktu pertemuan: Misalnya, Ani berlatih renang setiap 3 hari sekali, dan Budi berlatih renang setiap 4 hari sekali. Jika mereka berlatih renang bersama hari ini, kapan mereka akan berlatih renang bersama lagi? (Jawabannya adalah KPK dari 3 dan 4, yaitu 12 hari lagi).
• Mengatur jadwal: Misalnya, seorang apoteker ingin mengemas pil dalam botol. Ada 12 pil berwarna merah dan 18 pil berwarna biru. Apoteker ingin mengemas pil tersebut dalam botol sehingga setiap botol berisi jumlah pil merah dan biru yang sama. Berapa jumlah botol yang dibutuhkan? (Jawabannya adalah FPB dari 12 dan 18, yaitu 6 botol).

Contoh Penggunaan FPB:

• Membagi kelompok: Misalnya, seorang guru ingin membagi 24 siswa laki-laki dan 30 siswa perempuan menjadi beberapa kelompok. Guru ingin setiap kelompok memiliki jumlah siswa laki-laki dan perempuan yang sama. Berapa jumlah kelompok yang dapat dibentuk? (Jawabannya adalah FPB dari 24 dan 30, yaitu 6 kelompok).
• Menyederhanakan pecahan: FPB digunakan untuk menyederhanakan pecahan menjadi bentuk yang paling sederhana. Misalnya, pecahan 12/18 dapat disederhanakan menjadi 2/3 dengan membagi pembilang dan penyebut dengan FPB dari 12 dan 18, yaitu 6.

Tips dan Trik Belajar KPK dan FPB:

• Pahami Konsep Dasar: Pastikan Anda memahami dengan baik apa itu kelipatan, faktor, bilangan prima, dan faktorisasi prima.
• Latihan Soal: Semakin banyak latihan soal, semakin terbiasa Anda dengan berbagai jenis soal KPK dan FPB.
• Gunakan Metode yang Paling Nyaman: Pilih metode mencari KPK dan FPB yang paling Anda kuasai dan nyaman digunakan.
• Jangan Takut Bertanya: Jika Anda mengalami kesulitan, jangan ragu untuk bertanya kepada guru, teman, atau orang tua.
• Manfaatkan Sumber Belajar: Gunakan buku pelajaran, video pembelajaran, atau website edukasi untuk memperdalam pemahaman Anda tentang KPK dan FPB.

Kesimpulan:

KPK dan FPB adalah konsep penting dalam matematika yang memiliki banyak aplikasi dalam kehidupan sehari-hari. Dengan memahami konsep dasar, berlatih soal secara teratur, dan memanfaatkan berbagai sumber belajar, siswa kelas 4 SD dapat menguasai materi ini dengan baik dan merasa lebih percaya diri dalam belajar matematika. Selamat belajar!